ドアの選び方であなたの賢さが分かる!?――モンティ・ホール問題とは:現役東大生・森田徹の今週も“かしこいフリ”(2/3 ページ)
選び直す方が確率は上がる
この問題は一般的には「モンティ・ホール問題」と呼ばれており、米国では著名な経済学者や数学者を巻き込んで大論争になったこともある問題です。答えを先に言ってしまうと、ここではもう1枚のドアを選び直した方が当たる確率はグンと上がります。
私が初めてこの問題を聞いた時は、「残された2枚のドアから選び直す時は、どちらのドアを選んでも当たる確率は2分の1。よって、ドアを変えても変えなくても当たる確率は変わらない』と考えて、見事にひっかかってしまいました。私と同じように考えた人も少なくないのではないでしょうか? この問題を理由も含めて答えられる人は、かなり頭が切れると思います。
それでは実際にこのゲームをやってみて、ドアを選び直すと本当に当たる確率がアップするのか検証してみましょう。
3枚のドアを左・中央・右と名付けて考えます。そして、アタリが中央のドアだとします。最初にドアを選ぶ時には、ドアの選び方は3通りあります。そこで、それぞれの選択肢のときにどうすればアタリのドアまでたどり着けるかを考えてみましょう。
(1)最初に左のドアを選んだ時
司会者は残る2枚(中央と右)のドアのうち、ハズレの右のドアを開けます。この場合、あなたはドアを選び直すことでアタリのドアを選ぶことができます。
(2)最初に中央のドアを選んだ時
司会者は残る2枚(左と右)のドアのうち、どちらかのハズレのドアを開けます。この場合、司会者がどちらのドアを開けたとしても、あなたはドアを変更しなければアタリのドアを選ぶことができます。
(3)最初に右のドアを選んだとき
司会者は残る2枚(左と中央)のドアのうち、ハズレの左のドアを開けます。この場合、あなたはドアを選び直すことでアタリのドアを選ぶことができます。
(1)〜(3)より、アタリが中央のドアの時はドアを変更しないと当たる確率が3分の1、ドアを変更すると当たる確率が3分の2となり、ドアを選び直した方が2倍当たりやすくなります。ここでは省略しますが、アタリが左のドアでも右のドアでも同じ結果になります。
少し見方を変えてみましょう。最初に選んだドアが当たる確率は常に3分の1であり、選ばなかった残りの2枚のドアのどちらかが当たる確率は常に3分の2です。そして司会者は選ばなかった2枚のドアからわざとハズレのドアを開けてくれるわけです。すると、最初に選んだドアが当たる確率は3分の1のままですが、残ったもう1つのドアが当たる確率は3分の2になります。つまり、「ドアを選び直す」ということは「最初に選ばなかった2枚のドアを両方選ぶ」ということと同じになるのです。
ドアが100枚の場合で考えると……
このほかにもこの問題にはさまざまな説明の仕方があると思いますが、「言っていることは何となく分かるけどスッキリしない……」という人も少なくないでしょう。それはおそらく、人間の直感と確率論との間にズレが生じているからだと思います。しかし、自分が司会者になってゲームを進めていく場合をイメージしてみると、面白いくらいスッキリします。
ドアの枚数を3枚から100枚に増やした場合で考えてみましょう。ゲームの司会者であるあなたは100枚の中のどれがアタリかを知っています。それぞれのドアに1番から100番まで番号を付け、アタリが50番のドアでプレイヤーが10番のドアを選んだとします。すると、あなたは10番と50番を除くすべてのハズレのドアを1枚ずつ開けていきます。19番を開けて、89番を開けて、4番を開けて……、ハズレのドアを開けるにつれて残るドアの枚数はどんどん減っていきます。
こうして残りのドアが10番と50番の2枚になると、あなたはもう一度選び直すチャンスをプレイヤーに与えます。こうなると、ドアを選び直した方が当たる確率が明らかに高くなると感覚的にも思えるようになりませんか? この場合には、100枚のドアから最初に当たりのドアを選べたとき(確率はもちろん100分の1)以外には、ドアを選び直さないとアタリにはたどり着けないわけです。
Copyright © ITmedia, Inc. All Rights Reserved.
Special
PR注目記事ランキング
 モンティ・ホール問題
モンティ・ホール問題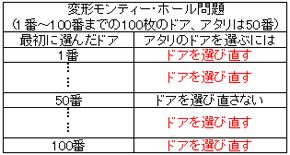 変形モンティ・ホール問題
変形モンティ・ホール問題


